PSU: Geometría |
Pregunta 08_2006
En la figura
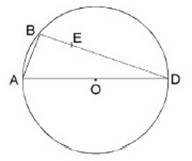
el lado AD del Δ ABD es el diámetro de la circunferencia de centro O . Para el punto E en el lado BD , se tiene que BE = 3, ED = 12 y AE = 6 .
El valor del radio es
Alternativas
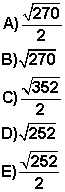
Comentario:
Para resolver correctamente la pregunta, el estudiante debe recordar que todo triángulo inscrito en una semicircunferencia ( Teorema de Tales ) es rectángulo.
En este caso el ∠ ABD = 90º y donde trazo AB y trazo BD son los catetos .
En el triángulo rectángulo AEB , que se forma al unir A con E, como se muestra en la figura,
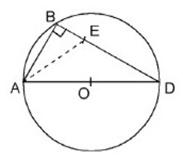
necesitamos calcular el cateto trazo AB .
Para ello aplicamos el Teorema de Pitágoras :
AE 2 = BE 2 + AB 2
6 2 = 3 2 + AB 2
AB
2
=6
2
– 3
2
, por lo que el valor del cateto
![]() .
.
Luego, para determinar el radio de la circunferencia, debemos calcular el diámetro de trazo AD, que es la hipotenusa del triángulo rectángulo ADB.
Utilizando nuevamente el Teorema de Pitágoras , se tiene:
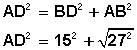
![]() , de donde el radio será
, de donde el radio será
![]()
.
Por lo cual la
clave es la opción E)
.
La pregunta resultó muy difícil, sólo el 14,1 por ciento la contestó correctamente y la omisión resultó altísima (72,5 por ciento), lo cual indica, posiblemente, que los estudiantes no reconocen fácilmente esta propiedad mencionada o no están habituados a resolver problemas donde tienen que trazar líneas adicionales para llegar a la solución.
Fuente Internet:
Publicación oficial del Demre en www.demre.cl

